This research article presents an analytical study of convective flow in a vertical channel with convective boundary conditions. Because of the nonlinear nature of the governing energy and momentum equations, the homotopy perturbation method was employed. The effects of various physical parameters on temperature and velocity profiles are illustrated in Figures 2 to 9, and a comparison table is provided to validate the results. Notably, both temperature and velocity distributions increased with higher viscous dissipation. Furthermore, the velocity profile decreased with an increase in the Biot number, while the temperature profile adjacent to the plate increased as the Biot number grew. Shear stress also exhibited an upward trend with rising viscous dissipation. Finally, an increase in the Grashof number and Biot number is found to elevate the skin friction on both plates. The mean temperature is higher when air is used as the working fluid compared to mercury. To validate this study, the temperature and velocity results were compared with previously published work, showing excellent agreement. This confirms the efficiency of the Homotopy Perturbation Method in solving coupled and nonlinear system of differential equations. Additionally, it was observed that both temperature and velocity increase with a rise in the Prandtl number, attributed to the dominance of momentum diffusivity over thermal diffusivity.
| Published in | International Journal of Fluid Mechanics & Thermal Sciences (Volume 10, Issue 3) |
| DOI | 10.11648/j.ijfmts.20241003.11 |
| Page(s) | 45-56 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Convective Boundary Condition, Couette Flow, Natural Convection, Viscous Dissipation, Homotopy Perturbation Method
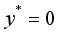 and
and 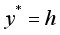 , where the hot and cold walls are maintained at uniform temperatures
, where the hot and cold walls are maintained at uniform temperatures 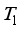 and
and 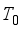 , respectively. It is assumed that the flow occur in the
, respectively. It is assumed that the flow occur in the 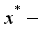 direction, vertically upward along the plates, while the
direction, vertically upward along the plates, while the 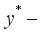 axis is perpendicular to the plates, as depicted in Figure 1. Given the infinite length of the plates, both the velocity and temperature fields are assumed to depend solely on the spatial coordinate.
axis is perpendicular to the plates, as depicted in Figure 1. Given the infinite length of the plates, both the velocity and temperature fields are assumed to depend solely on the spatial coordinate. 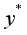 .
.  (1)
(1) 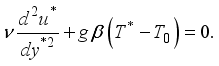 (2)
(2) 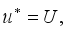
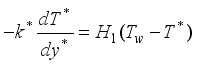 at
at 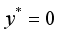
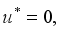
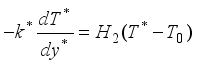 at
at 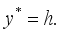 (3)
(3) 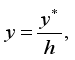
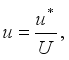
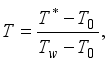
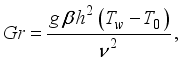

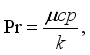
 (4)
(4) 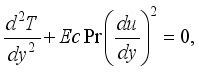 (5)
(5)  (6)
(6) 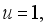
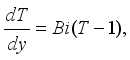 at
at 
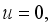
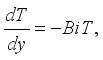 at(7)
at(7) 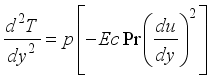 (8)
(8)  (9)
(9) 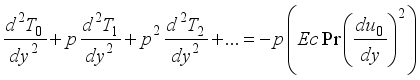

 (10)
(10) 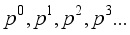 , we obtain
, we obtain  ,(11)
,(11)  (12)
(12)  (13)
(13) 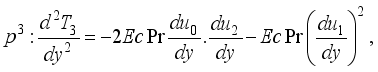 (14)
(14) 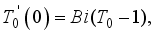

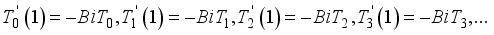 (15)
(15)  (16)
(16) 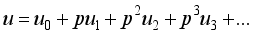 (17)
(17) 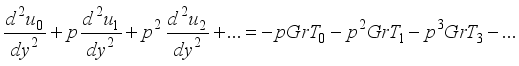 (18)
(18)  , we obtain
, we obtain  ,(19)
,(19)  (20)
(20) 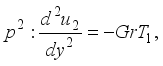 (21)
(21) 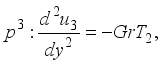 (22)
(22) 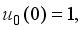
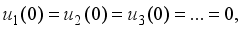
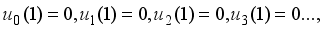 (23)
(23) 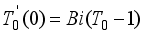 and
and 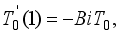
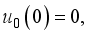 and
and 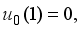 we obtain the solutions
we obtain the solutions  (24)
(24) 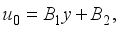 (25)
(25) 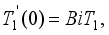 and
and 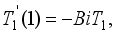
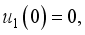 and
and 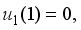 we obtain the solutions
we obtain the solutions 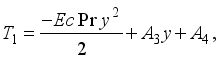 (26)
(26) 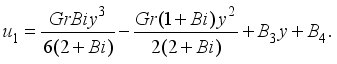 (27)
(27)  and
and 
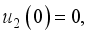 and
and 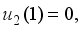 we obtain the solutions
we obtain the solutions 
 (28)
(28) 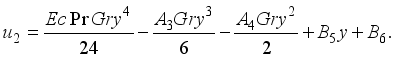 (29)
(29) 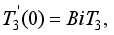 and
and 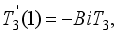
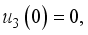 and
and 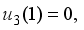 we obtain the solutions
we obtain the solutions 

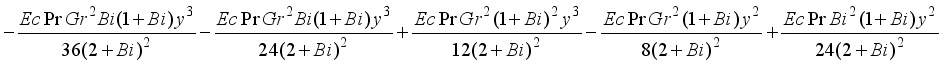

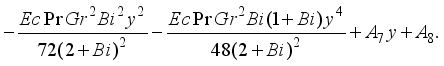 (30)
(30) 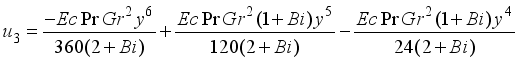
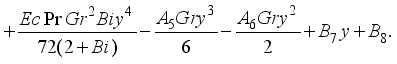 (31)
(31) 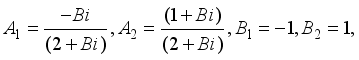
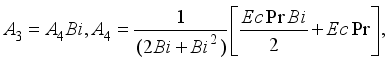
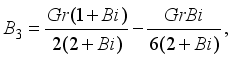




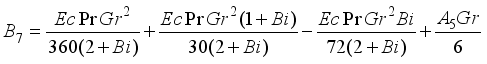
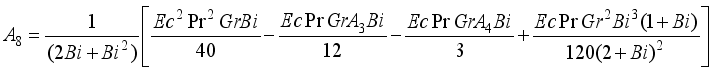
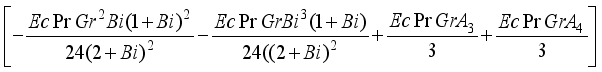
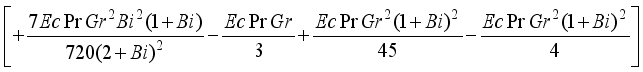
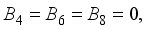
 and
and 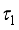 are expressed as follows:
are expressed as follows: 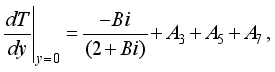
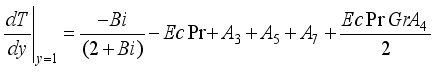
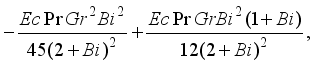
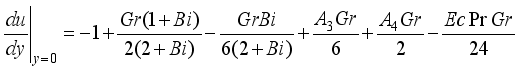

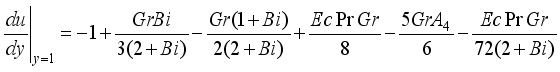
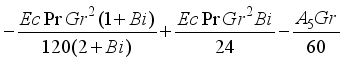
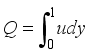 , we have
, we have 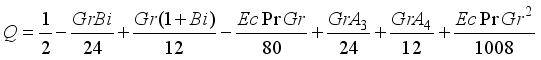
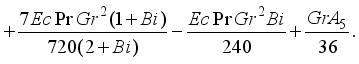
 ,
, 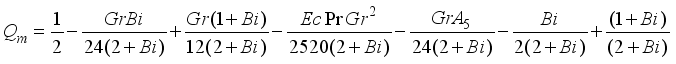
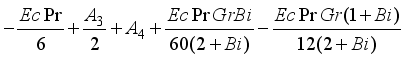 (32)
(32) Muawiya and Tafida [12] | Present problem | |||
|---|---|---|---|---|
Ec | Temperature | Velocity | Temperature | Velocity |
g | Acceleration to Due Gravity [ms-2] |
β | Coefficient of Thermal Expansion [K-1} |
h | Width of the Channel [m] |
μ | Coefficient of Viscosity [Kgm-1s-1] |
T* | Dimensional Fluid Temperature [K] |
ν | Kinematic Viscosity [m2s-1] |
Tw | Channel Wall Temperature [K] |
Pr | Prandtl Number |
T0 | Temperature of the Ambience [K] |
Gr | Grashof Number |
T | Dimensionless Fluid Temperature |
Ec | Eckert Number |
u* | Dimensional Velocity [ms-1] |
Bi | Biot Number |
u | Dimensionless Velocity |
cp | Specific Heat at Constant Pressure [m2s-2K-1] |
U | Dimensional Velocity of the Moving Plate [ms-1] |
ρ | Density of the Fluid [Kgm-3] |
y* | Coordinate Perpendicular to the Plate [m] |
α | Thermal Diffusivity of the Fluid [Kgm-3] |
y | Dimensionless Co-ordinate Perpendicular to the Plate |
| [1] | Momohjimoh, S. A., Oyem, O. A., Momoh, O. S., Onojovwo, T,. Felix. Convective heat and casson nanofluid flow over a vertical plate with heat source. Fudma Journal of Sciences. (2023), 7(2); 9 – 18. |
| [2] | Ajibade, A. O., Jeremiah, J. G., and Basant, K. J. Effect of darcy and viscous dissipation on natural convection flow in a vertical tube partially filled with porous material under convective boundary condition. International Journal of Applied Computational Mathematics. (2024), 10 – 84. |
| [3] | Agunbiade, S. A., and Oyekunle, S. A. Effects of magnetic field on natural convective steady flow past an irregular vertical channel in the presence of viscous dissipation. FUW Trends in Science and Technology Journal. (2019), 4(3); 666 – 670. |
| [4] | Tafida, M. K. and Ajibade, A. O. Variable viscosity and viscous dissipation effects on free convective Couette flow in a vertical channel: the homotopy perturbation method approach. (2020). The Journal of the Mathematical Association of Nigerian. 47(1), 161 – 175. |
| [5] | Ajibade, A. O., Tafida, M. K. Viscous dissipation effect on steady natural convection Couette flow with convective boundary condition. International Journal of Non-linear Sciences and Numerical Simulation. (2022), |
| [6] | Astanina, M. S., Mikhail, A. S. numerical study on natural convection of fluid with Temperature dependent viscosity. International Journal of Thermofluids. 2023, 100266. |
| [7] | Hussain, A., Isah, B. Y., and Zayyanu, S. Y. Impression of some fluid flow possession on unsteady conductive free convective fluid on account to dissipative porous walls. Himalayan Journal of Applied Medical Sciences and Research. 4(7), (2022), 31-52. |
| [8] | Ajibade, A. O., Ayuba, M. U., and Tafida, M. K. An analytical study on effects of viscous dissipation and suction/injection on a steady MHD natural convection Couette flow of heat generating/absorbing fluid. Advances in Mechanical Engineering. 13(5), (2021), 1-12. |
| [9] | Ajibade, A. O. and Tafida, M. K. Viscous dissipation effect of on steady natural Convection Couette flow with convective boundary condition. International Journal of Non-Linear Sciences and Numerical Simulation (IJNSNS). (2022), 7: 105 – 116. |
| [10] | Ajibade, A. O. and Princely, O. O. Effect of viscous dissipation on steady natural convection, heat and mass transfer in a vertical channel with variable viscosity and thermal conductivity. Journal of Heat and Mass Transfer Research. (2020). 7: 105 116. |
| [11] | Mehdi, M. and Kourosh, J. Viscous dissipation effect in the free convection of Non- Newtonian fluid with heat generation or absorption effect on the vertical wavy surface. Hindawi Journal of Applied Mathematics ID: 7567981, 14 pages. (2021): |
| [12] | Muawiya, H. U. and Tafida, M. K. Viscous dissipation effects on steady natural convection Couette flow in a vertical channel. Wudil Journal of Pure and Applied Sciences. (2019), 1(2), 169 – 179. |
| [13] | Isa, B. U., Yale, I. D., Sarki, M. N., and Hamza, M. M. Effects of viscous dissipative fluid on Couette flow in a vertical channel due to Newtonian heating. International Journal of Science for Global Sustainability. (2024), |
| [14] | Hamza, M. M. Navier slip and convective boundary condition effects on transient combined convection of dissipative fluid. The Transactions of the Nigerian Association Mathematical Physics. (2023), vol 19 (Jan – Dec issues). |
| [15] | Masthanaiah, Y., Nainaru, T., Ijaz, K. M., Rushikesava, S. M., Bandar, M. F., Sherzod, S., Abdullaer, S., and Sayed, M. E. Impact of viscous dissipation and entropy generation on cold liquid via channel with porous medium by analytical analysis. Case Studies in Thermal Engineering. (2023), 47; 103059. |
| [16] | Tafida, M. K., Ayuba, M. U., and Lawal, U. Magnetohydrodynamics free convection Couette flow and heat transfer through a vertical porous plate with heat generation and absorption effects. Dutse Journal of Pure and Applied Sciences. (2023), 9(2a); 133 - 145. |
| [17] | Ajibade, A. O., Ayuba, M. U. and Tafida, M. K. An Analytical study on effects of viscous dissipation and suction/injection on a steady MHD convection Couette flow of heat generating/absorbing fluid. Advances in Mechanical Engineering. (2021). 13(5), 1 – 12. |
| [18] | Liu, Z. J., Adamu, M. Y., Suleiman, E., and He, J. H. Hybridization of Homotopy Perturbation method and Laplace transformation for the partial differential equations. Thermal Science. (2017), 21; 1843 – 1846. |
| [19] | Abker, A. H. Solution of the linear and nonlinear Schrodinger equations using Homotopy Perturbation method and Iterative method. American Journal of Engineering Research. (2017), 6(3); 107 – 114. |
| [20] | Abou-Zeid, M. Homotopy Perturbation Method for Magnetohydrodynamics Non-Newtonian Nanofluid flow through a porous medium in eccentric annuli with peristalsis. Thermal Science. (2017), 21(5); 2069 – 2080. |
| [21] | Adamu, A. Y. Parameterized Homotopy Perturbation method. Nonlinear Science Letter A. (2017), 8(2); 240 – 243. |
| [22] | Ajibade, A. O. and Tafida, M. K. Effects of variability in viscosity and thermal conductivity Couette flow and heat transfer. Transactions of NAMP vol. 11, (January – June, 2020 Issue). |
| [23] | Nasution, H. Exploring of homotopy perturbation method (HPM) for Solving Spread of Covid-19. Jambura Journal of Biomathematics. (2023), 4(2); 138 – 154. |
APA Style
Kabir, T. M., Abdulganiyu, T. (2024). Homotopy Perturbation Method for Analyzing the Effect of Viscous Dissipation on Steady Natural Convection Couette Flow with Convective Boundary Conditions. International Journal of Fluid Mechanics & Thermal Sciences, 10(3), 45-56. https://doi.org/10.11648/j.ijfmts.20241003.11
ACS Style
Kabir, T. M.; Abdulganiyu, T. Homotopy Perturbation Method for Analyzing the Effect of Viscous Dissipation on Steady Natural Convection Couette Flow with Convective Boundary Conditions. Int. J. Fluid Mech. Therm. Sci. 2024, 10(3), 45-56. doi: 10.11648/j.ijfmts.20241003.11
AMA Style
Kabir TM, Abdulganiyu T. Homotopy Perturbation Method for Analyzing the Effect of Viscous Dissipation on Steady Natural Convection Couette Flow with Convective Boundary Conditions. Int J Fluid Mech Therm Sci. 2024;10(3):45-56. doi: 10.11648/j.ijfmts.20241003.11
@article{10.11648/j.ijfmts.20241003.11,
author = {Tafida Mohammed Kabir and Tajuddeen Abdulganiyu},
title = {Homotopy Perturbation Method for Analyzing the Effect of Viscous Dissipation on Steady Natural Convection Couette Flow with Convective Boundary Conditions
},
journal = {International Journal of Fluid Mechanics & Thermal Sciences},
volume = {10},
number = {3},
pages = {45-56},
doi = {10.11648/j.ijfmts.20241003.11},
url = {https://doi.org/10.11648/j.ijfmts.20241003.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijfmts.20241003.11},
abstract = {This research article presents an analytical study of convective flow in a vertical channel with convective boundary conditions. Because of the nonlinear nature of the governing energy and momentum equations, the homotopy perturbation method was employed. The effects of various physical parameters on temperature and velocity profiles are illustrated in Figures 2 to 9, and a comparison table is provided to validate the results. Notably, both temperature and velocity distributions increased with higher viscous dissipation. Furthermore, the velocity profile decreased with an increase in the Biot number, while the temperature profile adjacent to the plate increased as the Biot number grew. Shear stress also exhibited an upward trend with rising viscous dissipation. Finally, an increase in the Grashof number and Biot number is found to elevate the skin friction on both plates. The mean temperature is higher when air is used as the working fluid compared to mercury. To validate this study, the temperature and velocity results were compared with previously published work, showing excellent agreement. This confirms the efficiency of the Homotopy Perturbation Method in solving coupled and nonlinear system of differential equations. Additionally, it was observed that both temperature and velocity increase with a rise in the Prandtl number, attributed to the dominance of momentum diffusivity over thermal diffusivity.
},
year = {2024}
}
TY - JOUR T1 - Homotopy Perturbation Method for Analyzing the Effect of Viscous Dissipation on Steady Natural Convection Couette Flow with Convective Boundary Conditions AU - Tafida Mohammed Kabir AU - Tajuddeen Abdulganiyu Y1 - 2024/12/23 PY - 2024 N1 - https://doi.org/10.11648/j.ijfmts.20241003.11 DO - 10.11648/j.ijfmts.20241003.11 T2 - International Journal of Fluid Mechanics & Thermal Sciences JF - International Journal of Fluid Mechanics & Thermal Sciences JO - International Journal of Fluid Mechanics & Thermal Sciences SP - 45 EP - 56 PB - Science Publishing Group SN - 2469-8113 UR - https://doi.org/10.11648/j.ijfmts.20241003.11 AB - This research article presents an analytical study of convective flow in a vertical channel with convective boundary conditions. Because of the nonlinear nature of the governing energy and momentum equations, the homotopy perturbation method was employed. The effects of various physical parameters on temperature and velocity profiles are illustrated in Figures 2 to 9, and a comparison table is provided to validate the results. Notably, both temperature and velocity distributions increased with higher viscous dissipation. Furthermore, the velocity profile decreased with an increase in the Biot number, while the temperature profile adjacent to the plate increased as the Biot number grew. Shear stress also exhibited an upward trend with rising viscous dissipation. Finally, an increase in the Grashof number and Biot number is found to elevate the skin friction on both plates. The mean temperature is higher when air is used as the working fluid compared to mercury. To validate this study, the temperature and velocity results were compared with previously published work, showing excellent agreement. This confirms the efficiency of the Homotopy Perturbation Method in solving coupled and nonlinear system of differential equations. Additionally, it was observed that both temperature and velocity increase with a rise in the Prandtl number, attributed to the dominance of momentum diffusivity over thermal diffusivity. VL - 10 IS - 3 ER -