In the current context of climate change, solar energy stands out as a significant alternative to fossil fuels, which are both polluting and non-renewable. However, one of the main challenges in harnessing solar energy is the limited availability of data on solar radiation. Collecting solar radiation data through meteorological stations incurs considerable costs, unlike certain solar irradiation models that can provide such data for free. To facilitate access to solar irradiation information at no cost and to enhance the adoption and competitiveness of solar energy, it is crucial to develop practical daily global solar irradiation models that are applicable worldwide. This study aligns with that objective, aiming to develop a general model for estimating the maximum daily global solar irradiation. We use daily global solar irradiation data collected from 60 sites, spanning the years 2000 to 2023, for horizontal ground surfaces. To evaluate the performance of the proposed model, we conducted a detailed analysis using performance metrics. Two key indicators are highlighted in this manuscript: MAPE (Mean Absolute Percentage Error) and Pearson’s correlation coefficient. By utilizing daily global solar irradiation data from the 60 sites, empirical mathematical relationships for extraterrestrial daily solar irradiation, and computational tools, we established a mathematical expression for estimating maximum daily global solar irradiation. This model is specifically designed as a function of latitude and is independent of measured data such as sunshine duration, temperature, or humidity. Based on the performance indicators, the derived mathematical model demonstrates reasonable accuracy and a strong correlation.
| Published in | American Journal of Environmental Protection (Volume 14, Issue 1) |
| DOI | 10.11648/j.ajep.20251401.11 |
| Page(s) | 1-11 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Energy, Meteorological Stations, Global Solar Irradiation, Model, Performance
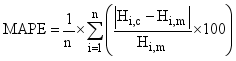 (1)
(1) values of MAPE (%) | Level of precision |
|---|---|
0 to 5 | Very good |
5 to 10 | Good |
10 to 20 | Fairly good |
20 to 30 | average |
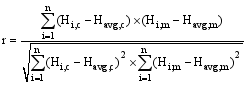 (2)
(2) Pearson's correlation coefficient values | Correlation quality |
|---|---|
0 to 0.1 | No correlation |
0.1 to 0.3 | Low correlation |
0.3 to 0.5 | Average correlation |
0.5 to 0.7 | High correlation |
0.7 to 1 | Very high correlation |
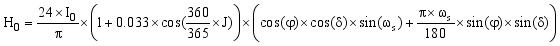 (3)
(3) 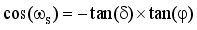 (4)
(4) 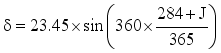 (5)
(5) 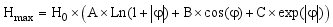 (6)
(6) Coefficient | -60 ≤ φ < 0 and 25 < φ ≤ 67 | 0 < φ ≤ 25 |
|---|---|---|
A | 0.53 | 0 |
B | 0.63 | 0.53 |
C | 0 | 0.153 |
Site | Latitude (°) | Longitude (°) | r for maximum data | MAPE for maximum data (%) |
|---|---|---|---|---|
Argentina - Ushuaia Aero | -54.8 N | -68.3 E | 0.98 | 15.58 |
Chile - Faro Evangelistas | -52.4 N | -75.1 E | 0.97 | 21.4 |
Argentina - Rio Gallegos Arpt | -51.6 N | -69.3 E | 0.99 | 4.89 |
Chile - Puerto Montt Tepual | -41.4 N | -73.1 E | 0.99 | 4.82 |
Chile - Temuco Maquehue | -38.8 N | -72.6 E | 0.99 | 3.04 |
Chile - Concepcion Carriel | -36.8 N | -73.1 E | 0.99 | 1.7 |
South Africa - Capetown | -34 N | 18.6 E | 0.99 | 1.6 |
Chile - Quelentaro | -34 N | -71.6 E | 0.99 | 2.74 |
Australia - WA - Ngaanyatjarra-Giles | -25 N | 128.3 E | 0.99 | 1.81 |
Australia - Alice Springs | -23.8 N | 133.9 E | 0.99 | 3.6 |
Chile - Antofagasta Cerro | -23.4 N | -70.4 E | 0.99 | 1.43 |
Namibia - Walvis Bay | -22.9 N | 14.4 E | 0.99 | 2.21 |
Chile - Calama | -22.5 N | -68.9 E | 0.99 | 9.65 |
Australia - Northern Territory-Tennant Creek | -19.6 N | 134.2 E | 0.99 | 2.84 |
Australia - Wyndham | -15.5 N | 128.1 E | 0.97 | 3.31 |
Zambia - Kabwe | -14.4 N | 28.5 E | 0.93 | 4.13 |
Brazil - Acre - Rio Branco Medici | -10 N | -67.8 E | 0.7 | 9.73 |
Brazil - Ceará - Barbalha | -7.3 N | -39.3 E | 0.9 | 5.28 |
Brazil - Amazonas - Tefe | -3.4 N | -64.7 E | 0.67 | 5.35 |
Gabon - Lambaréné | -0.7 N | 10.2 E | 0.51 | 20.27 |
Congo, Rép. Démocratique du - Boende | -0.2 N | 20.9 E | 0.74 | 4.41 |
Kenya - Nanyuki | 0 N | 37.1E | 0.79 | 5.67 |
Somalia - Mogadisho | 2 N | 45.3 E | 0.75 | 3.03 |
Ghana - Wenchi | 7.8 N | -2.1 E | 0.22 | 18 |
Somalia - Garōwe | 8.4 N | 48.5 E | 0.8 | 4.22 |
Burkina Faso - Gaoua | 10.3 N | -3.2 E | 0.6 | 5.01 |
Costa Rica - Puerto Limon | 10 N | -83.1 E | 0.76 | 11.7 |
India - Kerala - Kozhikode | 11.3 N | 75.8 E | 0.55 | 6.84 |
Sudan - Niyālā | 12.1 N | 24.9 E | 0.75 | 6.34 |
Burkina Faso - Ouagadougou | 12.4 N | -1.5 E | 0.83 | 4.32 |
Burkina Faso - Dori | 14 N | 0 E | 0.87 | 4.72 |
Honduras - Tegucigalpa Toncont | 14.1N | -87.2E | 0.83 | 4.86 |
Mexico - San Cristóbal de las Casas | 16.8N | -92.6E | 0.86 | 5.3 |
Niger - Arlit | 18.8 N | 7.3 E | 0.97 | 6.56 |
Mauritania - Šingati | 20 N | -12.4 E | 0.97 | 3.86 |
Algéria - Tamanrasset | 22.8 N | 5.4 E | 0.98 | 8.28 |
Japan - Minamitorishima | 24.3 N | 154 E | 0.99 | 1.46 |
India - Bihar - Patna | 25.6 N | 85.1 E | 0.91 | 9.21 |
Mexico - Monclova | 26.9 N | -101.4 E | 0.98 | 3.74 |
Algéria - Tindūf | 27.7 N | 8.2 E | 0.99 | 1.83 |
Saudi Arabia - Tabuk | 28.4 N | 36.6 E | 0.99 | 1.59 |
Saudi Arabia - Al-Jouf | 29.8 N | 40.1 E | 0.99 | 1.92 |
Mexico - Puerto Peñasco | 31.3 N | -113.5 E | 0.99 | 2.13 |
China - Henan - Nanyang | 33 N | 112.6 E | 0.97 | 9.84 |
United States of America - California | 34.3 N | -116.2 E | 0.99 | 3.11 |
United States of America - Nevada - Mercury | 36.6 N | -116 E | 0.99 | 3.96 |
China - Xinjiang - Andir | 37.9 N | 83.7 E | 0.99 | 4.11 |
Spain - Toledo | 39.9 N | -4.1 E | 0.99 | 1.65 |
China - Xinjiang - Urumqi | 43.8N | 87.7E | 0.99 | 2.77 |
Canada - Kejimkujik | 44.4 N | -65.2 E | 0.99 | 4.62 |
French - Paris Orly | 48.7 N | 2.4 E | 0.99 | 5.36 |
Kazakhstan - Turgaj | 49.6 N | 63.5 E | 0.99 | 3.87 |
Netherlands | 54.9 N | 4.7 E | 0.99 | 9.31 |
United States of America - Alaska - Hydaburg Seaplane | 55.2 N | -132.8 E | 0.99 | 6.83 |
Lituania - Laukuva | 55.6 N | 22.2 E | 0.99 | 8.01 |
Canada - Québec - Inukjuak | 58.5 N | -78.1 E | 0.99 | 14.1 |
Groenland - Narssarssuaq | 61.1 N | -45.4 E | 0.99 | 15.23 |
Russia - Surgut | 61.3 N | 73.5 E | 0.99 | 8.58 |
Canada - Nunavut | 64.2 N | -83.4 E | 0.98 | 15.16 |
United States of America - Alaska - Huslia | 65.7 N | -156.4 E | 0.99 | 12.45 |
RMSE | Root Mean Square Error |
ME | Mean Error |
PME | Mean Percentage Error |
MAPE | Mean Absolute Percentage Error |
MAE | Mean Absolute Error |
r | Pearson’s Correlation Coefficient |
R2 | Coefficient of Determination |
NASA | National Aeronautics and Space Administration |
ɷs | Sunset Hour Angle |
δ | Solar Declination Angle |
I0 | Solar Constant |
φ | Latitude |
| [1] | M. Tunç, U. Çamdali, T. Liman, A. Deger, «Electrical energy consumption and production of Turkey versus world», Energy Policy 34 (2006) 3284–3292, |
| [2] | H. Benli, «Potential of renewable energy in electrical energy production and sustainable energy development of Turkey: Performance and policies», Renewable Energy 50 (2013) 33e46, |
| [3] | B. Multon, «L’énergie électrique: analyse des ressources et de la production», Journées électrotechniques du Club EEA Paris 28-29 janvier 1999. |
| [4] | S. Paraschiv, «Analysis of the variability of low-carbon energy sources, nuclear technology and renewable energy sources, in meeting electricity», Energy Reports 9 (2023) 276–283, |
| [5] | B. Zohuri, P. McDaniel, «Chapter 6 - Other electrical power generation energy sources», Introduction to Energy Essentials (2021), 223-254, |
| [6] | J. Wang, W. Azam, «Natural resource scarcity, fossil fuel energy consumption, and total greenhouse gas emissions in top emitting countries», Geoscience Frontiers 15 (2024) 101757, |
| [7] | K. R. Abbasi, K. Hussain, M. Redulescu, I. Ozturk, «Does natural resources depletion and economic growth achieve the carbon neutrality target of the UK? A way forward towards sustainable development». Resour. Policy 74 (2021) 102341. |
| [8] | D. Bonkoungou, J. M. Ilboudo, A. Kabre, Z. Koalaga, «Monitoring and Effectiveness Analysis of a Hybrid PV Battery System in Real Conditions», International Journal of Energy and Power Engineering, 2023; 12(6): 75-83, |
| [9] | J. M. Ilboudo, D. Bonkoungou, Z. Koalaga, «A New Approach to Sizing PV Modules While Accounting the Effect of Temperature», American Journal of Energy Engineering, 2023; 11(4): 127-133, |
| [10] | A. Angström, «Solar and Terrestrial Radiation», Quarterly journal of the Royal Meteorological Society, vol. 50, n° 210, 1924, pp. 121–126, |
| [11] | M. Paulescu, N. Stefu, D. Calinoiu, E. Paulescu, N. Pop, R. Boata, O. Mares, «Ångström–Prescott equation: Physical basis, empirical models and sensitivity analysis», Renewable and Sustainable Energy Reviews 62 (2016) 495–506, |
| [12] | Mohamed Salah Mecibah, Taqiy Eddine Boukelia, Reda Tahtah, Kacem Gairaa, «Introducing the best model for estimation the monthly mean daily global solar radiation on a horizontal surface (Case study: Algeria)», Renewable and Sustainable Energy Reviews 36 (2014) 194–202, |
| [13] | C. Iradukunda, K. Chiteka, «Angstrom-Prescott Type Models for Predicting Solar Irradiation for Different Locations in Zimbabwe», Journal of Mechanical Engineering 69(2023)1-2, 32-48, |
| [14] | H. Morf, «A stochastic solar irradiance model adjusted on the Angström–Prescott regression», Solar Energy 87 (2013) 1–21, |
| [15] | Muhammad Jamilu Ya’u, Muhammad Abdullahi Gele, Yerima Yusif Ali, Abdulkarim Mika’il Alhaji, «Global Solar Radiation Models: A Review», Journal of Photonic Materials and Technology, 2018, 4(1): 26-32, |
| [16] | H. Ögelman, A. Ecevit, E. Tasdemiroglu, «A new method for estimating solar radiation from bright sunshine data», Solar Energy 1984; 33: 619–25, |
| [17] | F. Besharat, A. A. Dehghan, A. R. Faghih, «Empirical models for estimating global solar radiation: A review and case study», Renewable and Sustainable Energy Reviews 21 (2013) 798–821, |
| [18] | T. D. M. A. Samuel, «Estimation of global radiation for Sri Lanka», Solar Energy Vol. 47, No. 5, pp. 333-337, 1991, |
| [19] | D. B. Ampratwum, A. S. S. Dorvlo, «Estimation of solar radiation from the number of sunshine hours», Applied Energy 63 (1999) 161-167, |
| [20] | J. Almorox, C. Hontoria, «Global solar radiation estimation using sunshine duration in Spain», Energy Conversion and Management 45 (2004) 1529–1535, |
| [21] | K. Bakirci, «Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey», Energy 34 (2009) 485–501, |
| [22] | Hargreaves GH, Samani ZA, «Estimating potential evapotranspiration», Journal of Irrigation and Drainage Engineering, 1982; 108(IR3): 223–230, |
| [23] | R. Chen, K. Ersi, J. Yang, S. Lu, W. Zhao, «Validation of five global radiation models with measured daily data in China», Energy Conversion and Management 2004; 45: 1759–1769, |
| [24] | C. K. Pandey, A. K. Katiyar, «Temperature base correlation for the estimation of global solar radiation on horizontal surface», IJEE.2010; 1: 737–44. |
| [25] | B. Benamrou, O. Mustapha, I. Allaouzi, M. B. Ahmed «Empirical models for estimating the global solar radiation based on air temperature and sunshine duration», 2018 Association for Computing Machinery, ACM ISBN 978-1-4503-6562-8/18/10, |
| [26] | K. BRISTOW and G. S. CAMPBELL, «On the relationship between incoming solar radiation and daily maximum and minimum temperature», Agricultural and Forest Meteorology, 31 (1984) 159-166, |
| [27] | R. K. Swartman and O. Ogunlade, «Solar Radiation Estimates from Common Parameters», Presented at the Solar Energy Conference, Tempe, Arizona, March 20-22, 1967, |
| [28] | A. A. El-Sebaii, A. A. Al-Ghamdi, F. S. Al-Hazmi, A. S. Faidah, «Estimation of global solar radiation on horizontal surfaces in Jeddah, Saudi Arabia», Energy Policy 37 (2009) 3645–3649, |
| [29] | K. K. Gopinathan, «A new model for estimating total solar radiation», Solar & Wind Technology Vol. 5, No. L pP. 107-109, 1988, |
| [30] | Y. A. G. ABDALLA, «New correlations of global solar radiation with meteorological parameters for bahrain», Inr. J. Solar Energy. 1994, Val. 16, pp. I 1 1-120, |
APA Style
Ilboudo, J. M., Bonkoungou, D., Ouedraogo, W. R., Tassembedo, S., Koalaga, Z. (2025). An Improved Approach for Maximum Daily Global Solar Irradiance Estimation. American Journal of Environmental Protection, 14(1), 1-11. https://doi.org/10.11648/j.ajep.20251401.11
ACS Style
Ilboudo, J. M.; Bonkoungou, D.; Ouedraogo, W. R.; Tassembedo, S.; Koalaga, Z. An Improved Approach for Maximum Daily Global Solar Irradiance Estimation. Am. J. Environ. Prot. 2025, 14(1), 1-11. doi: 10.11648/j.ajep.20251401.11
@article{10.11648/j.ajep.20251401.11,
author = {Jacques Marie Ilboudo and Dominique Bonkoungou and Wilfried Rimnogdo Ouedraogo and Sosthene Tassembedo and Zacharie Koalaga},
title = {An Improved Approach for Maximum Daily Global Solar Irradiance Estimation
},
journal = {American Journal of Environmental Protection},
volume = {14},
number = {1},
pages = {1-11},
doi = {10.11648/j.ajep.20251401.11},
url = {https://doi.org/10.11648/j.ajep.20251401.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajep.20251401.11},
abstract = {In the current context of climate change, solar energy stands out as a significant alternative to fossil fuels, which are both polluting and non-renewable. However, one of the main challenges in harnessing solar energy is the limited availability of data on solar radiation. Collecting solar radiation data through meteorological stations incurs considerable costs, unlike certain solar irradiation models that can provide such data for free. To facilitate access to solar irradiation information at no cost and to enhance the adoption and competitiveness of solar energy, it is crucial to develop practical daily global solar irradiation models that are applicable worldwide. This study aligns with that objective, aiming to develop a general model for estimating the maximum daily global solar irradiation. We use daily global solar irradiation data collected from 60 sites, spanning the years 2000 to 2023, for horizontal ground surfaces. To evaluate the performance of the proposed model, we conducted a detailed analysis using performance metrics. Two key indicators are highlighted in this manuscript: MAPE (Mean Absolute Percentage Error) and Pearson’s correlation coefficient. By utilizing daily global solar irradiation data from the 60 sites, empirical mathematical relationships for extraterrestrial daily solar irradiation, and computational tools, we established a mathematical expression for estimating maximum daily global solar irradiation. This model is specifically designed as a function of latitude and is independent of measured data such as sunshine duration, temperature, or humidity. Based on the performance indicators, the derived mathematical model demonstrates reasonable accuracy and a strong correlation.
},
year = {2025}
}
TY - JOUR T1 - An Improved Approach for Maximum Daily Global Solar Irradiance Estimation AU - Jacques Marie Ilboudo AU - Dominique Bonkoungou AU - Wilfried Rimnogdo Ouedraogo AU - Sosthene Tassembedo AU - Zacharie Koalaga Y1 - 2025/01/21 PY - 2025 N1 - https://doi.org/10.11648/j.ajep.20251401.11 DO - 10.11648/j.ajep.20251401.11 T2 - American Journal of Environmental Protection JF - American Journal of Environmental Protection JO - American Journal of Environmental Protection SP - 1 EP - 11 PB - Science Publishing Group SN - 2328-5699 UR - https://doi.org/10.11648/j.ajep.20251401.11 AB - In the current context of climate change, solar energy stands out as a significant alternative to fossil fuels, which are both polluting and non-renewable. However, one of the main challenges in harnessing solar energy is the limited availability of data on solar radiation. Collecting solar radiation data through meteorological stations incurs considerable costs, unlike certain solar irradiation models that can provide such data for free. To facilitate access to solar irradiation information at no cost and to enhance the adoption and competitiveness of solar energy, it is crucial to develop practical daily global solar irradiation models that are applicable worldwide. This study aligns with that objective, aiming to develop a general model for estimating the maximum daily global solar irradiation. We use daily global solar irradiation data collected from 60 sites, spanning the years 2000 to 2023, for horizontal ground surfaces. To evaluate the performance of the proposed model, we conducted a detailed analysis using performance metrics. Two key indicators are highlighted in this manuscript: MAPE (Mean Absolute Percentage Error) and Pearson’s correlation coefficient. By utilizing daily global solar irradiation data from the 60 sites, empirical mathematical relationships for extraterrestrial daily solar irradiation, and computational tools, we established a mathematical expression for estimating maximum daily global solar irradiation. This model is specifically designed as a function of latitude and is independent of measured data such as sunshine duration, temperature, or humidity. Based on the performance indicators, the derived mathematical model demonstrates reasonable accuracy and a strong correlation. VL - 14 IS - 1 ER -